组合优化问题关心如何找到离散优化问题的最优解，在科学和工程领域有广泛的应用。很多组合优化问题，例如旅行商问题、图染色问题等都是NP难问题，也许并不存在一般性高效率的求解方法。

　　统计物理中关心的自旋玻璃模型的基态问题也属于NP难的组合优化问题。为此，物理学家们发明了各种各样的严格和近似的方法来寻找系统的基态。此外，当自旋玻璃模型的基态存在简并时，严格计算基态的个数(即零点熵)属于更难的一类被称为#P难的问题。在最近的工作中， 中科院理论物理研究所张潘研究员与哈佛大学博士后刘金国，中科院物理所王磊研究员合作，提出了一种基于张量网络的严格求解组合优化问题最优解和零点熵的方法。

　　这个工作将张量网络收缩中的加乘运算替换为定义在极大-加法半环上的“热带”代数(Tropical Algebra)，称之为热带张量网络(Tropical Tensor Network)。“热带”代数首先由巴西科学家Imre Simon提出，“热带”一词体现了给这类代数命名的法国科学家对于巴西的印象。通过收缩热带张量网络，可以计算自旋玻璃模型的基态能量和熵，从而直接研究零温下的统计物理问题。结合机器学习中的可微分编程，此方法可以充分发挥量子线路模拟器Yao.jl和高效并行计算设备GPU的计算能力。作者利用此方法研究了二维、三维、随机图，以及D-wave公司量子退火计算机上所使用的Chimera图上的自旋玻璃模型，以及Potts玻璃模型和最大约束满足等物理和计算机科学中的组合优化问题。在一些情况下Tropical张量网络方法比例如分支界定等传统计算方法算得更快且可以求解更大尺寸的问题。这项进展融合了统计物理、张量网络、机器学习以及量子计算等领域中的概念与方法，为求解组合优化问题提供了新工具和新思路。

　　下图为此算法在富勒烯图上所定义的自旋玻璃模型中所找到的基态构型。

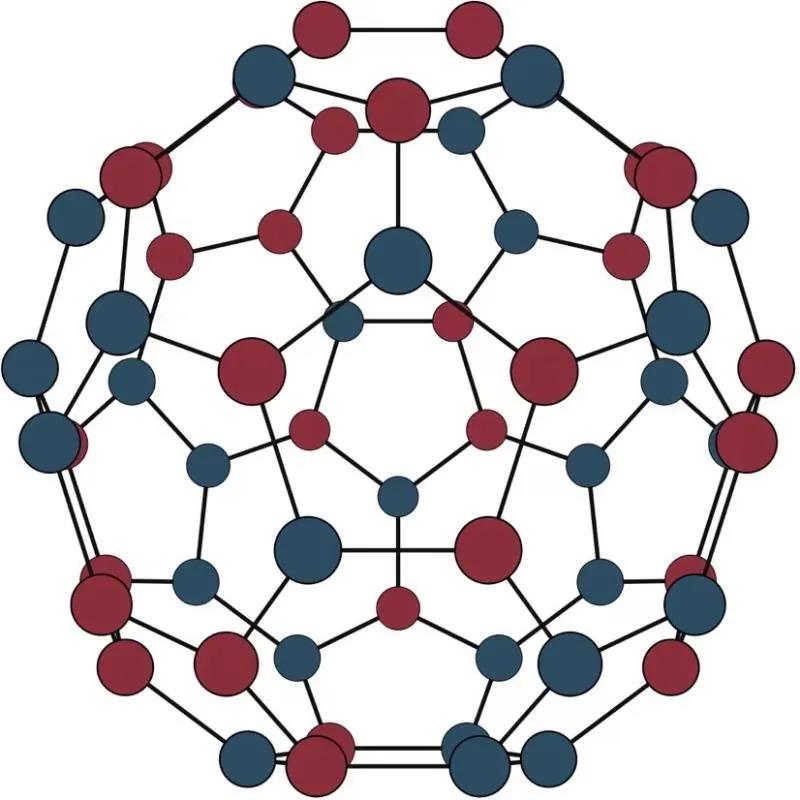
　　该工作近期发表于物理评论快报[Phys. Rev. Lett. 126, 090506 (2021)]。

　　论文链接：

　　https://link.aps.org/doi/10.1103/PhysRevLett.126.090506

　　开源实现见：

　　https://github.com/TensorBFS/TropicalTensors.jl

　　另可参考刘金国博士编写的教学程序：

　　https://giggleliu.github.io/notebooks/tropical/tropicaltensornetwork.html